Bank menurut Undang-undang Nomor 10 Tahun 1998 tentang Perbankan merupakan badan usaha yang menghimpun dana dari masyarakat dalam bentuk simpanan dan menyalurkannya kepada masyarakat dalam bentuk kredit dan atau bentuk-bentuk lainnya dalam rangka meningkatkan taraf hidup masyarakat.

Bank disini berperan sebagai perantara (financial intermediary) antara pihak yang kelebihan uang (surplus) sebagai penabung/deposan dan bidang yang kekurangan uang (defisit). Pemberian pinjaman ini disebut dengan pembiayaan tidak langsung (indirect financing).

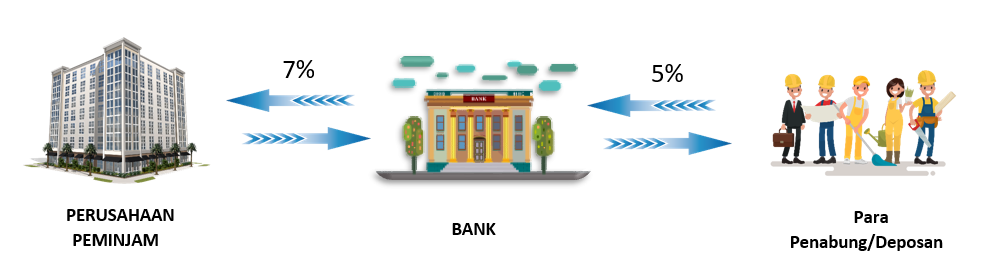
Bank mendapatkan spread atau net interest margin sebesar 2% (7% diperoleh dari pinjaman – 5% bunga yang dibayarkan oleh bank kepada penabung/deposan) sebagai jasa perantara keuangan. Negara yang sistem keuangannya didominasi pembiayaan seperti ini disebut negara dengan sistem berbasis bank atau bank – based seperti di Indonesia dan jepang.

Seiring dengan berkembangnya zaman dimana peminjam berusaha meminimumkan biaya bunga, sedangkan pihak yang kelebihan dana ingin memaksimumkan pendapatan bunga maka keduaanya disatukan dengan menghilangkan peranan Bank sebagai perantara keuangan. Disini peminjam (emiten) mengeluarkan surat utang sebagai bukti utang yang disebut obligasi untuk diberikan kepada pemberi pinjaman atau investor. Jadi pembiayaan seperti ini disebut Pembiayaan langsung (direct financing).

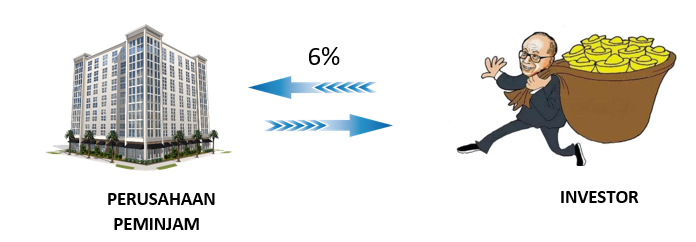
Kedua pihak lebih diuntungkan karena peminjam lebih suka membayar 6% daripada 7% dan investor lebih suka menerima 6% daripada 5%. Negara yang sistem keuangannya lebih mengandalkan pembiayaan seperti ini disebut negara dengan sistem keuangan berbasis pasar atau marked based seperti Amerika serikat dan Inggris.

Seiring dengan perbaikan jenis pembiayaan maka muncul pembiayaan semi langsung (semidirect financing method). Proses ini pemindahan atau pertukaran dana antara debitur atau kreditur sangat tergantung pada intervensi pihak ketiga, yaitu broker, dealer, investment banker. Suatu perusahaan menerbitkan obligasi maka perusahaan bersangkutan sangat tergantung kepada peran dealer sekuritas dalam hal penjualan seluruh surat berharga yang diterbitkan kepada investor (rumah tangga, perusahaan, bank, asuransi, dana pension). Broker/dealer dalam pembiayaan ini dapat mengurangi biaya transaksi, biaya informasi dan memperbaiki likuiditas dan kemampuan pemasaran surat berharga yang terciptadari proses pinjam-meminjam.

Definisi Obligasi (Bond)

Obligasi (Bond) artinya surat utang jangka panjang yang dikeluarkan peminjam (emiten) kepada pemberi pinjaman (investor) (Frensidy, 2016:303). Surat utang ini berisi janji dari yang menerbitkan (penjual/debitur) kepada pembeli (kreditur/investor) untuk membayar imbalan berupa bunga (kupon) dan pokok pinjaman pada waktun yang ditentukan. Obligasi merupakan jenis investasi yang relatif stabil, bukan jenis risiko yang tinggi (high risk).

Emiten adalah perusahaan baik swasta atau BUMN yang mencari modal dari bursa efek dengan cara menerbitkan efek. Emiten memang bisa berupa perusahaan swasta atau BUMN, baik itu perusahaan terbuka maupun perusahaan tertutup. Karena itu, emiten wajib telah melakukan Initial Public Offering (IPO) alias go public sebelumnya. Obligasi dapat diterbitkan oleh Korporasi maupun Negara (IDX).

Jenis-Jenis Obligasi

Jenis-jenis obligasi antara lain:

Obligasi berdasarkan sisi penerbit
- Obligasi Pemerintah

Obligasi pemerintah adalah surat utang yang diterbitkan pemerintah (negara). Surat utang ini sah secara hukum dan dilindungi berbagai peraturan, termasuk undang-undang, peraturan pemerintah, peraturan menteri keuangan (PMK), dan lainnya. Jenis investasi ini lebih aman dari risiko gagal bayar sehingga banyak diincar investor. Obligasi jenis ini biasanya diterbitkan setiap 1 tahun sekali. Jenis obligasi dalam obligasi pemerintah antara lain:

- - Obligasi Negara Ritel Indonesia (ORI)
  - Obligasi Negara Ritel atau ORI merupakan salah satu instrumen Surat Berharga Negara (SBN) yang ditawarkan kepada individu atau perseorangan Warga Negara Indonesia melalui Mitra Distribusi di Pasar Perdana.
  - Sukuk Ritel (SukRi)
  - Sukuk Ritel adalah produk investasi syariah yang ditawarkan oleh Pemerintah kepada individu Warga Negara Indonesia, sebagai pilihan investasi yang aman, mudah, terjangkau, dan menguntungkan.

Sukuk Ritel dikelola berdasarkan prinsip syariah, tidak mengandung unsur maysir (judi) gharar (ketidakjelasan) dan riba (usury), serta telah dinyatakan sesuai syariah oleh Dewan Syariah Nasional – Majelis Ulama Indonesia (DSN-MUI).

Penerbitan Sukuk Ritel menggunakan struktur akad Ijarah – Asset to be Leased. Dana hasil penerbitan akan digunakan untuk kegiatan investasi berupa pembelian hak manfaat Barang Milik Negara untuk disewakan kepada Pemerintah serta pengadaan proyek untuk disewakan kepada Pemerintah. Imbalan berasal dari keuntungan hasil kegiatan investasi tersebut.

- - Tujuan utama penerbitan Sukuk Ritel adalah untuk membiayai APBN dan membiayai pembangunan proyek infrastruktur di Indonesia.
  - Contoh Sukri untuk proyek pembangunan gedung perkuliahan PTKIN, Gedung Asrama Haji, Jembatan dsb.
  - Saving Bond Ritel (SBR)
    Surat utang negara atau obligasi negara dengan jangka waktu 2 tahun yang sifatnya mirip tabungan karena harus disimpan hingga jatuh tempo dan tidak bisa diperdagangkan dipasar sekunder, Namun SBR dapat dilakukan pencairan awal (early redemption) setelah 12 bulan.
  - Sukuk Negara Tabungan (ST)

Green Sukuk Ritel – Sukuk Tabungan merupakan penerbitan Green Sukuk Ritel pertama sekaligus menunjukkan komitmen dan kontribusi Pemerintah dalam mengembangkan pasar keuangan Syariah dan juga dalam mengatasi perubahan iklim, yang diwujudkan melalui penerbitan instrumen pembiayaan yang inovatif dan berkelanjutan. Tujuan pembiayaan ini untuk proyek ramah lingkungan di dua sektor yakni Transportasi berkelanjutan dan Ketahanan terhadap perubahan iklim. Hal ini diharapkan dapat memitigasi dampak perubahan iklim dan adaptasi atas perubahan iklim yang telah terjadi

Surat utang dengan nama depan sukuk berarti surat utang yang berbasis syariah.

- Obligasi Pemerintah Daerah

Obligasi Pemerintah daerah adalah surat utang yang diterbitkan oleh pemerintah daerah, namun tidak dijamin oleh Pemerintah. Tujuan penerbitaan obligasi jenis ini adalah membantu pemerintah daerah dalam membiayai kegiatan pemerintah daerah guna menghasilkan penerimaan dan manfat bagi masyarakat daerah. Jenis obligasi daerah adalah obligasi pendapatan (Revenue Bond).

- Obligasi Korporasi

Obligasi Korporasi adalah obligasi yang diterbitkan oleh korporasi atau perusahaan, baik perusahaan BUMN atau korporasi dari pihak swasta. Jenis obligasi korporasi antara lain obligasi kupon tetap, obligasi dengan kupon variabel dan obligasi dengan prinsip syariah.

Jenis Obligasi Berdasarkan Pembayaran Bunga (Kupon)
- Zero coupon bonds (obligasi tanpa kupon)
  Obligasi tanpa kupon merupakan obligasi yang tidak memberikan kupon secara berkala. Investor akan menerima bunga dan pokok keuntungan secara penuh sekaligus saat jatuh tempo sesuai dengan timeline yang tertera pada surat pernyataan utang tersebut.
- Fixed coupon bonds (obligasi kupon tetap)
  Obligasi kupon tetap adalah obligasi yang memberikan keuntungan berupa kupon tetap secara berkala, nilai atau persentase bunga yang akan dibayarkan secara periodik tetap sesuai dengan persetujuan sebelum masa penawaran perdana saat obligasi ini diterbitkan.
- Variable coupon bonds (obligasi kupon variabel)
  Obligasi kupon variabel hampir sama dengan obligasi kupon tetap namun, obligasi ini memberikan keuntungan (kupon) dapat berubah sewaktu-waktu yang dipengaruhi oleh acuan dari suku bunga perbankan.
Jenis Obligasi Berdasarkan Jaminan
- Secured Bonds

Secured bonds adalah obligasi yang dijaminkan dengan kekayaan milik penerbit atau bisa juga dijaminkan pihak ketiga. Nantinya, dana penjualan obligasi akan digunakan untuk membeli aset tertentu lalu aset dipinjamkan ke perusahaan. Jenis obligasi ini dibagi menjadi tiga:

- - Mortgage bonds adalah obligasi dengan jaminan berupa gedung atau bangunan
  - Collateral trust bonds adalah obligasi yang dijaminkan dengan saham atau obligasi milik penerbit
  - Equipment trust certificate adalah obligasi yang digunakan untuk mendanai berbagai aset, seperti pesawat, gerbong kereta, atau truk.
- Unsecured Bonds

Unsecured bonds adalah jenis obligasi yang tidak dijaminkan menggunakan kekayaan milik penerbit. Obligasi jenis ini dibagi menjadi tiga:

- - Debentures adalah obligasi yang hanya diterbitkan perusahaan yang sudah terpercaya.
  - Subordinated debentures adalah obligasi ini tidak akan dibayar jika obligasi yang lebih senior dibayarkan.
  - Income bonds adalah obligasi diterbitkan yang mana perusahaan membayar bunga ketika memperoleh laba. Obligasi ini biasa untuk mereorganisasi perusahaan yang dianggap kurang berhasil.

**Obligasi Berbunga (Coupon bond)**

Obligasi berbunga (coupon bond) adalah obligasi yang memberikan bunga secara periodik kepada pemegangnya (Frensidy, 2016:305). Obligasi berbunga atau obligasi kupon adalah surat utang yang secara berkala memberikan bunga kepada pihak investornya. Obligasi berbunga berisi:

Nilai nominal, yaitu besarnya utang yang akan dilunasi pada saat jatuh tempo.
Tanggal jatuh tempo, yaitu tanggal pelunasan utang obligasi.
Tingkat bunga obligasi atau kupon, biasanya dalam persentase dan dinyatakan per tahun (p.a.).
Tanggal pembayaran bunga, menjelaskan apakah bunga obligasi dibayar setahun sekali atau setahun dua kali (per setengah tahun).

Obligasi memiliki sifat likuid, artinya obligasi dapat dijual belikan setiap hari di Bursa Efek Indonesia (BEI). Imbal hasil obligasi disebut yield. Harga obligasi dalam yang diperdagangkan biasanya dinyatakan dengan angka persentase (tanpa %). Misal harga penutupan obligasi adalah 105, berarti obligasi itu diperdagangkan pada 105% dari harga nominal.

Di Indonesia kupon SBN dibayarkan setiap enam bulan, kupon korporasi setiap tiga bulan, sedangkan kupon ORI (Obligasi Negara Ritel) dan Sukri (Sukuk Ritel) dibayar setiap bulan.

Penentuan Harga Wajar (Fair Price)

Harga wajar obligasi adalah jumlah nilai sekarang (present value) dari anuitas (cicilan) bunga yang dibayarkan dan nilai sekarang dari nilai nominalnya.

P = $\frac{[1-(1+i)^{-n}]C}{i}+\frac{F}{(1+i)^{n}}$

atau

Harga wajar obligasi adalah selisih antara bunga (yield) yang diharapkan dan kupon yang dibayarkan. Kemudian menghitung nilai sekarang dari anuitas (cicilan) selisih bunga ini ditambah dengan nilai nominalnya.

P = $F +(c-i)F\frac{[1-(1+i)^{-n}]}{i}$

Dimana:
F = nilai nominal atau nilai pari obligasi
c = tingkat bunga (kupon) obligasi per periode
C = pembayaran bunga per periode (tingkat bunga kupon (c) x nominal)
n = jumlah periode
P = harga wajar obligasi
i = Yield per periode

Yield adalah tingkat pengembalian investasi bagi seorang investor yang dinyatakan dalam persentase

Contoh soal 1: Perusahaan mengeluarkan sebuah obligasi bernilai nominal Rp 200.000.000 dengan bunga J2=10% jatuh tempo dalam 5 tahun. Tentukan harga wajar obligasi jika perusahaan mengharapkan yield:
a. 12% p.a
b. 8% p.a

Diketahui:
F = 200.000.000
j2 = 10% =>
c = 10%/2 = 5% = 0,05
C = 5% x 200.000.000 = 10.000.000
n = 5 tahun x 2 (karena j2/bunga diperhitungkan 2x setahun-persemester) = 10

Ditanya: P / nilai wajar / fair value

Dijawab:
a. Jika yield = 12% p.a => i = 12%/2 = 6% =0,06

Cara 1
P = $\frac{[1-(1+i)^{-n}]C}{i}+\frac{F}{(1+i)^{n}}$
P = $\frac{[1-(1+0,06)^{-10}]10.000.000}{0,06}+\frac{200.000.000}{(1+0,06)^{10}}$
P = $\frac{[1-(1,06)^{-10}]10.000.000}{0,06}+\frac{200.000.000}{(1,06)^{10}}$
P = $\frac{[1-0,5584]10.000.000}{0,06}+\frac{200.000.000}{1,7908}$
P = $\frac{[0,4416]10.000.000}{0,06}+{111.678.955,38}$
P = $\frac{4.416.000}{0,06}+{111.678.955,38}$
P = 73.600.870,51 +111.678.955,38
P = 185.279.825,90

Cara 2

P = $F +(c-i)F\frac{[1-(1+i)^{-n}]}{i}$
P = $200.000.000 +(0,05-0,06)200.000.000\frac{[1-(1+0,06)^{-10}]}{0,06}$
P = $200.000.000 +(-0,01)200.000.000\frac{[1-(1,06)^{-10}]}{0,06}$
P = $200.000.000 - 2.000.000.000\frac{[1-0,5584]}{0,06}$
P = $200.000.000 - 2.000.000.000\frac{[0,4416]}{0,06}$
P = 200.000.000 – 2.000.000.000 x 7,3601
P = 200.000.000 – 14.720.174,10
P = 200.000.000 – 14.720.174,10
P = 185.279.825,90

b. Jika yield = 8% p.a => i = 8%/2 = 4% = 0,04

Cara 1
P = $\frac{[1-(1+i)^{-n}]C}{i}+\frac{F}{(1+i)^{n}}$
P = $\frac{[1-(1+0,04)^{-10}]10.000.000}{0,04}+\frac{200.000.000}{(1+0,04)^{10}}$
P = $\frac{[1-(1,04)^{-10}]10.000.000}{0,04}+\frac{200.000.000}{(1,04)^{10}}$
P = $\frac{[1-0,6756]10.000.000}{0,06}+\frac{200.000.000}{1,4802}$
P = $\frac{0,3244 x 10.000.000}{0,06}+135.112.833,77$
P = $\frac{3.244.000}{0,06}+135.112.833,77$
P = 81.108.957,79+135.112.833,77
P = 216.221.791,56

Cara 2

P = $F +(c-i)F\frac{[1-(1+i)^{-n}]}{i}$

P = $200.000.000 +(0,05-0,04)200.000.000\frac{[1-(1+0,04)^{-10}]}{0,04}$
P = $200.000.000 +0,01 x 200.000.000\frac{[1-(1,04)^{-10}]}{0,06}$
P = $200.000.000 + 2.000.000.000\frac{[1-0,6756]}{0,04}$
P = $200.000.000 + 2.000.000.000\frac{[0,3244]}{0,04}$
P = 200.000.000 + 2.000.000.000 x 8,1109
P = 200.000.000 + 16.221.791,56
P = 216.221.791,56

**Obligasi Tidak Berbunga (Zero Coupon bond)**

Yaitu obligasi yang tidak membayar bunga secara periodik dan hanya membayar nilai nominal saat jatuh tempo. Dalam hal menarik minat para investor, obligasi jenis ini dijual dengan diskon yang sangat besar sehingga disebut deep discount bond. Harga wajar dari obligasi ini dinyatakan dengan persamaan:

P = $\frac{F}{(1+i)^{n}}$

Dimana:
F = nilai nominal atau nilai pari obligasi
n = jumlah periode
P = harga wajar obligasi
i = yield per periode

Contoh soal 2: Sebuah obligasi tak berbunga yang bernilai nominal Rp 400.000.000 dan jatuh tempo dalam 5 tahun. Tentukan harga wajar obligasi jika investor mengharapkan yield J2=18% !

Diketahui
F = 400.000.000
i = 18% / 2 =0,09
n = 5 x 2 = 10

Ditanya: Nilai wajar (P)?

P = $\frac{F}{(1+i)^{n}}$
P = $\frac{400.000.000}{(1+0,09)^{10}}$
P = $\frac{400.000.000}{(1,09)^{10}}$
P = $\frac{400.000.000}{2,3673}$
P = 168.964.322,76

Jadi harga wajar obligasi jika investor mengharapkan yield J2=18% adalah Rp 168.964.322,76

**Obligasi Dapat Ditebus (Callable bond)**

Callable bond yaitu obligasi yang dapat ditebus sebelum jatuh tempo. Hak untuk menebus obligasi yang dilakukan emiten digunakan jika menguntungkan misalnya keadaan tingkat bunga pasar sudah turun dan lebih rendah daripada tingkat bunga obligasi.

Callable bond menimbulkan masalah dalam menghitung harga wajar karena jangka waktu obligasi sehingga dilunasi menjadi tidak pasti. Investor harus menghitung harga obligasi yang menjamin yield yang diinginkan dapat tercapai dengan atau tanap digunakannya hak penebusan oleh emiten.

Contoh soal 3: PT Rids menerbitkan Obligasi dengan nilai nominal Rp 1 miliar berjangka waktu 10 tahun dengan kupon J2 = 12% tetapi dapat ditebus pada nilai pari setelah 5 tahun. Hitung harga pembelian yang menjamin investor mendapat yield minimum:
a. J2=14%
b. J2=8%

Diketahui:
F = 1.000.000.000
n = 10 x 2 = 20
npenebusan= 5 x 2 =10
J2 = 12%
c = 12%/2 =6%= 0,06
C = 6% x 1.000.000.000 = 60.000.000

Ditanya: P / nilai wajar / fair value

Dijawab:
a. Harga pembelian yang menjamin investor mendapat yield minimum J2=14%

i = 14%/2 =7%= 0,07

harga wajar jika obligasi ditebus setelah 5 tahun

P = $F +(c-i)F\frac{[1-(1+i)^{-n}]}{i}$
P = $1.000.000.000 +(0,06-0,07) x 1.000.000.000 x \frac{[1-(1+0,07)^{-10}]}{0,07}$
P = $1.000.000.000 +(-0,01) x 1.000.000.000 x \frac{[1-0,508349]}{0,07}$
P = $1.000.000.000 +(-10.000.000) x \frac{[0,491651]}{0,07}$
P = 1.000.000.000 +(-10.000.000 x 7,023582)
P = 1.000.000.000 +(-70.235.815,41)
P = 929.764.184,59

Harga wajar obligasi dilunasi saat jatuh tempo 10 tahun:

P = $F +(c-i)F\frac{[1-(1+i)^{-n}]}{i}$
P = $1.000.000.000 +(0,06-0,07) x 1.000.000.000 x \frac{[1-(1+0,07)^{-20}]}{0,07}$
P = $1.000.000.000 +(-0,01) x 1.000.000.000 x \frac{[1-0,25841]}{0,07}$
P = $1.000.000.000 +(-10.000.000) x \frac{[0,74158]}{0,07}$
P = 1.000.000.000 +(-10.000.000 x 10,59401)
P = 1.000.000.000 +(-105.94o.142)
P = 894.059.858

Jadi harga pembelian yang menjamin investor mendapat yield minimum J2=14% adalah Rp 894.059.858

b. Harga pembelian yang menjamin investor mendapat yield minimum J2=8%

i = 8%/2=4%=0,04

harga wajar jika obligasi ditebus 5 tahun

P = $F +(c-i)F\frac{[1-(1+i)^{-n}]}{i}$
P = $1.000.000.000 +(0,06-0,04) x 1.000.000.000 x \frac{[1-(1+0,04)^{-10}]}{0,04}$
P = $1.000.000.000 +(0,02) x 1.000.000.000 x \frac{[1-0,675564169]}{0,04}$
P = $1.000.000.000 +(20.000.000) x \frac{[0,324435831]}{0,04}$
P = 1.000.000.000 +(20.000.000 x 8,110895779)
P = 1.000.000.000 + 162.217.915,59
P = 1.162.217.915,59

Harga wajar obligasi dilunasi saat jatuh tempo 10 tahun:

P = $F +(c-i)F\frac{[1-(1+i)^{-n}]}{i}$
P = $1.000.000.000 +(0,06-0,04) x 1.000.000.000 x \frac{[1-(1+0,04)^{-20}]}{0,04}$
P = $1.000.000.000 +(0,02) x 1.000.000.000 x \frac{[1-0,45638]}{0,04}$
P = $1.000.000.000 +(20.000.000) x \frac{[0,54361]}{0,04}$
P = 1.000.000.000 +(20.000.000) x 13,59032
P = 1.000.000.000 +271.806.527
P = 1.271.806.527

Harga pembelian yang menjamin investor mendapat yield minimum J2=8% adalah P=1.162.217.915,59

Contoh soal 4: PT Alufam menerbitkan obligasi dengan nilai pari Rp 400.000.000 berjangka waktu 25 tahun dengan bunga J2 = 16%. Obligasi itu dapat ditebus pada akhir tahun ke-10 pada harga 110 atau pada akhir tahun ke-15 pada harga 105. Berapa harga obligasi yang menjamin investor memperoleh yield minimum J2=12%?

Diketahui:
F = F25 = 400.000.000
n = 25 x 2 = 50
n penebusan ke-10 = 10 x 2 =20
F10 = 400.000.000 x 110% = 440.000.000,00
npenebusan ke-15= 15 x 2 =30
F15 = 400.000.000 x 105%= 420.000.000,00
J2 = 16% => c = 16%/2 =8%= 0,08
C = 8% x 400.000.000 = 32.000.000
i = 12%/2=6%=0,06

Ditanya: P / nilai wajar / fair value
Dijawab:
Harga wajar obligasi ditebus setelah 10 tahun:

P = $\frac{[1-(1+i)^{-n}]C}{i}+\frac{F10}{(1+i)^{n}}$
P = $\frac{[1-(1+0,06)^{-20}]32.000.000}{0,06}+\frac{440.000.000}{(1+0,06)^{20}}$
P = $\frac{[1-0,31180] x 32.000.000}{0,06}+\frac{440.000.000}{3,20713}$
P = $\frac{0,68819x 32.000.000}{0,06}+ 137.194.080$
P = $\frac{22.022.248,7}{0,06}+ 137.194.080$
P = 367.037.478,9+ 137.194.080
P = 504.231.558,8

Harga wajar obligasi ditebus setelah 15 tahun:

P = $\frac{[1-(1+i)^{-n}]C}{i}+\frac{F15}{(1+i)^{n}}$
P = $\frac{[1-(1+0,06)^{-30}]32.000.000}{0,06}+\frac{420.000.000}{(1+0,06)^{30}}$
P = $\frac{[1-0,17411] x 32.000.000}{0,06}+\frac{420.000.000}{5,74349}$
P = $\frac{0,82589x 32.000.000}{0,06}+ 73.126.255$
P = $\frac{26.428.475,8}{0,06}+ 73.126.255$
P = 440.474.596,8+ 73.126.255
P = 513.600.851,8

Harga wajar obligasi ditebus setelah 25 tahun:

P = $\frac{[1-(1+i)^{-n}]C}{i}+\frac{F25}{(1+i)^{n}}$
P = $\frac{[1-(1+0,06)^{-50}]32.000.000}{0,06}+\frac{400.000.000}{(1+0,06)^{50}}$
P = $\frac{[1-0,054288] x 32.000.000}{0,06}+\frac{400.000.000}{18,42015}$
P = $\frac{0,94571 x 32.000.000}{0,06}+ 21.715.345$
P = $\frac{30.262.772,4}{0,06}+ 21.715.345$
P = 504.379.540,3+ 21.715.345
P = 526.094.885

Jadi harga obligasi yang menjamin investor memperoleh yield minimum J2=11% adalah harga terendah dari ketiga harga diatas yaitu: 504.231.558,8.

Amortisasi Premium dan Diskon Obligasi

Untuk harga wajar dari setiap obligasi yang diperdagangkan dipengaruhi oleh yield yang diharapkan investor. Ada beberapa kemungkinan yang terjadi yaitu:

Jika yield sama dengan bunga obligasi yang dibayarkan maka harga wajar obligasi adalah nilai nominal obligasi (nilai Pari)

Contoh 5: Misal: Perusahaan mengeluarkan sebuah obligasi bernilai nominal Rp 200.000.000 dengan bunga J2 = 10% jatuh tempo dalam 5 tahun. Tentukan harga wajar obligasi jika perusahaan mengharapkan yield 10% p.a

Jawab
F = 200.000.000
c = 10%/2 = 5% = 0,05
C = 5% x 200.000.000 = 10.000.000
n = 5 tahun x 2 = 10
i = 10%/2 = 5% = 0,05

P = $F +(c-i)F\frac{[1-(1+i)^{-n}]}{i}$

P = $200.000.000 +(0,05-0,05)200.000.000\frac{[1-(1+0,06)^{-10}]}{0,06}$
P = $200.000.000 +(0)200.000.000\frac{[1-(1,06)^{-10}]}{0,06}$
P = 200.000.000 + 0
P =200.000.000

Jika yield lebih rendah dari bunga obligasi maka harga obligasi diatas nilai nominal dan dapat juga dikatakan obligasi dijual dengan premium.

Contoh 6: Perusahaan mengeluarkan sebuah obligasi bernilai nominal Rp 200.000.000 dengan bunga J2 = 10% jatuh tempo dalam 5 tahun. Tentukan harga wajar obligasi jika perusahaan mengharapkan yield 8% p.a
Jawab
F = 200.000.000
c = 10%/2 = 5% = 0,05
C = 5% x 200.000.000 = 10.000.000
n = 5 tahun x 2 = 10
i = 8%/2 = 4% = 0,04

P = $F +(c-i)F\frac{[1-(1+i)^{-n}]}{i}$
P = $200.000.000 +(0,05-0,04)200.000.000\frac{[1-(1+0,04)^{-10}]}{0,04}$
P = $200.000.000 +0,01 x 200.000.000\frac{[1-(1,04)^{-10}]}{0,06}$
P = $200.000.000 + 2.000.000.000\frac{[1-0,6756]}{0,04}$
P = $200.000.000 + 2.000.000.000\frac{[0,3244]}{0,04}$
P = 200.000.000 + 2.000.000.000 x 8,1109
P = 200.000.000 + 16.221.791,56
P = 216.221.791,56

Jika yield lebih besar dari bunga obligasi maka harga obligasi dibawah nilai nominal dan dapat dikatakan harga dijual dengan diskon.

Contoh: 7 Perusahaan mengeluarkan sebuah obligasi bernilai nominal Rp 200.000.000 dengan bunga J2 = 10% jatuh tempo dalam 5 tahun. Tentukan harga wajar obligasi jika perusahaan mengharapkan yield 12% p.a
Jawab
F = 200.000.000
c = 10%/2 = 5% = 0,05
C = 5% x 200.000.000 = 10.000.000
n = 5 tahun x 2 = 10
i = 12%/2 = 6% = 0,06

Dapat disimpulkan kemungkinan harga wajar yang terjadi dapat diilustrasi di antara tiga obligasi yang memiliki tiga harga yang berbeda yaitu:

obli

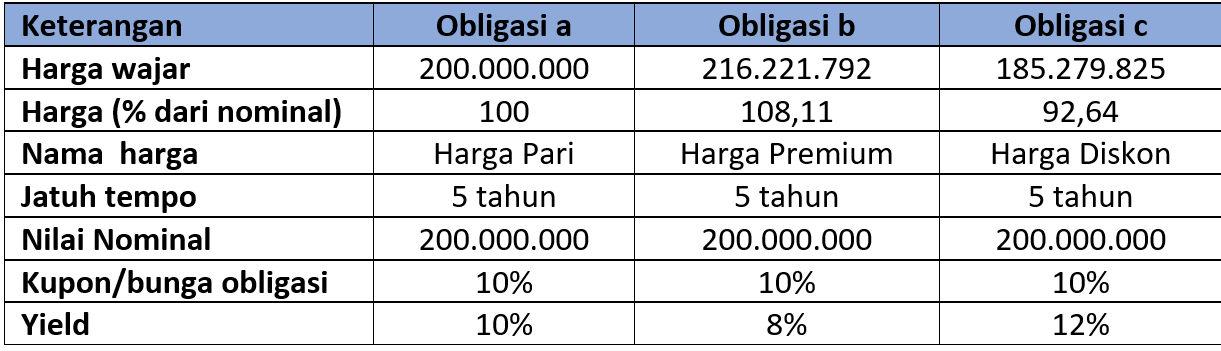
Contoh Kasus Lima tahun lalu, Pak Didi membeli obligasi ABCD dengan kupon 10% dengan harga 100 dengan nilai Rp100.000.000. Pak Didi membeli obligasi itu dengan harapan dapat mendapatkan keuntungan setelah pajak sekitar Rp 8,5 juta per tahun atau sekitar Rp4,25 juta per 6 bulan. Dalam 5 tahun, Pak Didi menerima keuntungan sekitar Rp 42,5 juta (5 tahun dikali Rp8,5 juta per tahun).

Sebelum jatuh tempo, Pak Didi membutuhkan uang untuk merenovasi rumah. Pak Didi kemudian berpikir untuk menjual obligasinya. Pada saat itu, harga obligasi sebesar 98. Apabila Pak Didi menjual obligasi tersebut di harga 98 apakah dia mengalami kerugian dari investasi tersebut?

Jawabannya tidak.

Jika Dalam 5 tahun, dia telah mendapatkan keuntungan dari kupon yang dibayar setiap tahun atau 2 kali setiap 6 bulan yaitu Rp8,5 juta per tahun. Pergerakan harga tidak mempengaruhi nilai kupon yang diterima oleh investor.

Pada saat menjual obligasi di harga 98, dia akan mengalami capital loss sebesar 2 juta (dari perhitungan Rp100.000.000 x (98-100) %). Namun jika kerugian itu dikompensasi dari keuntungan yang telah diperoleh setiap tahun dari kupon (8,5 juta per tahun) masih untung Rp 6,5 juta per tahun (8,6 juta – 2 juta).

Jadi untuk menilai apakah suatu investasi itu merugi atau laba seharusnya kita mengetahui terlebih dahulu nilai kupon yang didapat dan nilai kerugian atau keuntungan saat menjual kembali obligasi.

Pada saat jatuh tempo, semua obligasi akan dilunasi pada nilai parinya. Dengan kata lain, premium dan diskon obligasi yang ada harus menjadi nol atau habis pada saaat jatuh tempo. Penyesuaian nilai premium dan diskon obligasi secara periodik dicatat dalam laporan keuangan emiten (perusahaan yang menerbitkan obligasi) hingga tidak ada lagi (atau 0) pada saat jatuh tempo disebut amortisasi premium/diskon atau amortisasi agio/disagio.

Contoh soal 8. Susun tabel amortisasi sebuah obligasi bernilai nominal Rp 400.000.000, jatuh tempo 10 tahun lagi dengan kupon j1 = 14% jika investor mengharapkan yield 8% p.a.

Diketahui:
F              = 400.000.000
c              = 14% /1 = 14% = 0,14
C             = c x F = 14% x 400.000.000        = 56.000.000
n             = 10 tahun x 1 periode = 10
i               = 8%/1 = 8% = 0,08

Ditanya: Tabel Amortisasi

P = $F +(c-i)F\frac{[1-(1+i)^{-n}]}{i}$
P = $400.000.000 +(0,14-0,08)400.000.000\frac{[1-(1+0,08)^{-10}]}{0,08}$
P = $400.000.000 +(0,06)400.000.000\frac{[1-(1,08)^{-10}]}{0,08}$
P = $400.000.000 + 24.000.000\frac{[1-0,46319]}{0,08}$
P = $400.000.000 + 24.000.000\frac{[0,5368]}{0,08}$
P = 400.000.000 + 24.000.000 x 6,71
P = 400.000.000 + 161.041.953,57
P =561.041.953,57

Tabel amortisasi atas obligasi yang mempunyai harga premium dengan metode bunga efektif

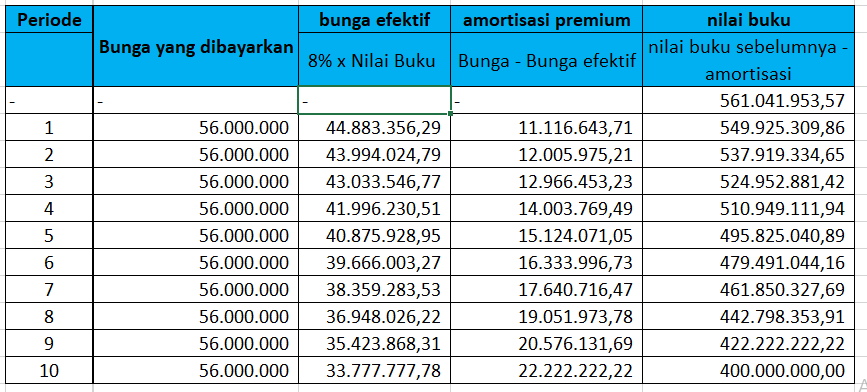
Tabel amortisasi atas obligasi yang mempunyai harga premium dengan metode Garis lurus

Amortisasi premium = (harga wajar – harga nominal) / periode

= (561.041.953,57 – 400.000.000) / 10
= 161.041.953,57/10
= 16.104.195.36

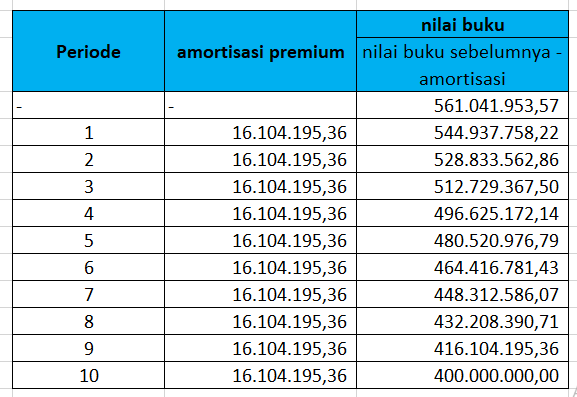
Contoh soal 9: Susun tabel amortisasi sebuah obligasi bernilai nominal Rp 800.000.000 yang dikeluarkan pada 1 januari 2019 dan jatuh tempo lima tahun lagi dengan kupon j2 = 8%. Jika investor mengharapkan yield 16 % p.a. Hitung juga nilai buku obligasi per 1 juli 2021.

jawab:

F              = 800.000.000
c              = 8% /2 = 4%    = 0,04
C             = c x F
                = 4% x 800.000.000        = 32.000.000
n             = 5 tahun x 2 periode = 10
i               = 16%/1                = 8% = 0,08

P = $F +(c-i)F\frac{[1-(1+i)^{-n}]}{i}$
P = $800.000.000 +(0,04-0,08)800.000.000\frac{[1-(1+0,08)^{-10}]}{0,08}$
P = $800.000.000 +(-0,04)800.000.000\frac{[1-(1,08)^{-10}]}{0,08}$
P = $800.000.000 - 32.000.000\frac{[1-0,46319]}{0,08}$
P = $800.000.000 - 32.000.000\frac{[0,5368]}{0,08}$
P = 800.000.000 – 32.000.000 x 6,71
P = 800.000.000 – 214.722.604,77
P =585.277.395,23

Tabel amortisasi atas obligasi yang mempunyai harga diskon dengan metode bunga efektif

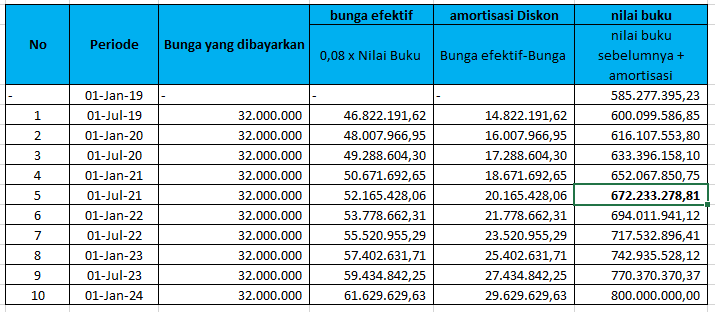
Tabel amortisasi atas obligasi yang mempunyai harga diskon dengan metode Garis lurus

Amortisasi premium = ( harga nominal – harga wajar ) / periode

= (800.000.000 – 585.277.395,23) / 10
= 214.722.604,77/10
= 21.472.260,48

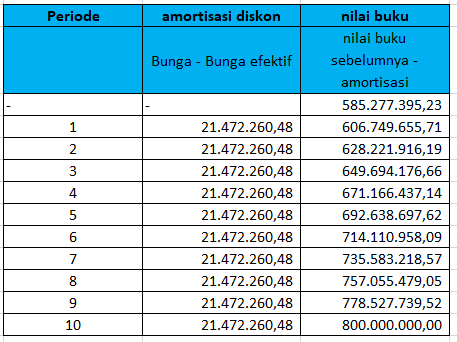
Nilai obligasi per 1 juli 2021 adalah

n = 2,5 x 2 periode = 5

P = $F +(c-i)F\frac{[1-(1+i)^{-n}]}{i}$
P = $800.000.000 +(0,04-0,08)800.000.000\frac{[1-(1+0,08)^{-5}]}{0,08}$
P = $800.000.000 +(-0,04)800.000.000\frac{[1-(1,08)^{-5}]}{0,08}$
P = $800.000.000 - 32.000.000\frac{[1-0,68058]}{0,08}$
P = $800.000.000 - 32.000.000\frac{[0,31942]}{0,08}$
P = 800.000.000 – 32.000.000 x 3,99271
P = 800.000.000 – 127.766.721,19
P =672.233.278,81

Jadi nilai buku obligasi per tanggal per 1 juli 2021 adalah Rp 672.233.278,81

Harga Obligasi Diantara Dua Tanggal Pembayaran Bunga

Obligasi diperdagangkan setiap hari kerja di Bursa Efek Indonesia dengan nilai transaksi harian mencapai belasan triliun rupiah. Dengan demikian, kita perlu mengetahui metode menghitung harga wajar obligasi pada tanggal lainnya. Kebiasaan dalam praktik perdagangan obligasi adalah pembeli membayar kepada penjual bunga yang terkandung dalam obligasi, yaitu bunga yang belum dibayarkan dari tanggal pembayaran bunga terakhir hingga tanggal transaksi. Dalam akuntansi, bunga terkandung ini disebut bunga terutang (accrued interest). Pembeli bersedia membayarkan bunga terutang ini kepada penjual karena pembeli akan menerima bunga secara penuh pada tanggal pembayaran bunga berikutnya.

Untuk menghitung harga wajar obligasi yang diperjualbelikan antara dua tanggal pembayaran bunga, kita akan menggunakan persamaan:

P = P₀ x (1+i)^fBunga terutang = AI = f x C
Pq = P – AI

Dimana:

P             = harga yang harus dibayarkan pembeli atau harga kotor (dirty price)
P₀ = harga wajar obligasi pada tanggal pembayaran bunga terakhir
f              = jumlah hari yang telah lewat sejak tanggal pembayaran bunga terakhir dibagi dengan total jumlah hari
antara dua tanggal pembayaran bunga (yang lalu dan yang berikutnya)
Pq           = harga yang penawaran obligasi di pasar (market quitation) dan tidak termasuk bunga atau disebut harga
bersih (clean price)

Contoh soal 10

Sebuah obligasi bernilai nominal Rp 1 milyar dengan kupon j2 =10% dan jatuh tempo pada 15 Agustus 2014. Obligasi ini dijual pada tanggal 1 September 2014 dengan harga penawaran pasar (market quotation) 105. Berapa yang harus dibayar pembeli, jika bunga dibayar setiap tanggal 1 Februari dan 15 Agustus?

Jawab

Tanggal-tanggal pembayaran : 1 februari dan 15 agustus

Jumlah hari antara tanggal 15 agustus 2014 dan 1 februari 2015 adalah 170 hari.
Jumlah hari dari tanggal 15 agustus 2014 hingga 1 september 2014 adalah 17 hari

Jadi bunga terutang adalah:

f              = 17/170 = 0,1
F              = 1.000.000.000
c              = 10 % / 2           =5 %               = 0,05

Harga yang harus dibayar pembeli adalah

P = Pq + AI

= (harga penawaran pasar x F )+ (f x C)
= (harga penawaran pasar x F )+ (f x c x F)
= (105 % x 1.000.000.000) + (0,1 x 0,05 x 1.000.000.000)
= 1.050.000.000 + 5.000.000
= 1.055.000.000

LATIHAN SOAL

Daftar Pustaka

Frensidy, Budi. 2019. Matematika Keuangan, Edisi keempat, Jakarta: Salemba Empat.

https://www.idx.co.id/id/produk/surat-utang-obligasi

pngwing.com

https://www.ojk.go.id/id/kanal/perbankan/pages/Bank-Umum.aspx#:~:text=Pada%20Undang%2Dundang%20Nomor%2010,rangka%20meningkatkan%20taraf%20hidup%20masyarakat.

https://www.kemenkeu.go.id/ori

https://www.kemenkeu.go.id/sukukritel

https://www.kemenkeu.go.id/sukuktabungan

https://www.kemenkeu.go.id/SBR

https://www.bareksa.com/berita/sbn/2022-05-17/sbr011-segera-terbit-ini-pengertian-sbr-dan-cara-daftarnya-di-bareksa

Obligasi Daerah

CORE ACCOUNTING INDONESIA

OBLIGASI (BOND)