Perbedaan antara anuitas biasa (ordinary annuity) anuitas dimuka (annuity due) adalah saat pembayaran pertama. Pada anuitas biasa pembayaran pertama dilakukan pada satu periode yang akan datang atau satu periode setelahnya. Sedangkan pada anuitas dimuka pembayaran dilakukan pada awal periode atau hari ini.
Anuitas yang sering digunakan adalah anuitas biasa. Perhitungan anuitas biasa menghasilkan nilai yang hampir sama untuk periode yang besar. Namun, untuk periode yang lebih pendek, hasilnya cukup berbeda. Aplikasi yang hampir pasti menggunakan anuitas dimuka adalah kontrak leasing jangka panjang atau kontrak capital lease.
Nilai Sekarang Anuitas Di Muka
Menghitung Nilai Sekarang (PVDUE) Menggunakan Cara Manual
PVDUE = \frac{[1-(1+i)^{-(n-1)}]}{i} A + A
PVDUE ={ {\frac{1-(1+i)^{-n+1}}{i}+1} }x A
Dimana:
PVDUE : nilai sekarang (present value) anuitas di muka
i : tingkat bunga per periode
n : jumlah periode
A : anuitas atau pembayaran per periode
Menghitung Nilai PVDUE Menggunakan Ms. Excel
=PVDUE(rate;Nper;Pmt;FV;Type)
Rate : tingkat bunga (misalkan dihitung per bulan maka dibagi 12 dan dikasih tanda %)
Nper : jumlah periode
PMT : jumlah pembayaran berkala yang tetap/anuitas (diberi tanda minus)
FV opsional : Nilai masa yang akan datang atau keseimbangan kas yang ingin Anda capai setelah pembayaran terakhir dilakukan. Jika fv dikosongkan, maka diasumsikan sebagai 0 (nol), yaitu, nilai pinjaman yang akan datang adalah 0.
Type : 1 jika pembayaran dilakukan pada awal periode
Menghitung Nilai PVDUE Menggunakan Financial Calculator
Untuk mencari nilai sekarang menggunakan aplikasi financial calculators dapat menggunakan time value of money (TVM) dengan langkah-langkah berikut:
1. Buka aplikasi financial calculators
2. Pilih TVM calculator (pada pojok kiri atas)
3. Masukkan angka-angka yang diketahui
-
- Payment untuk pembayaran cicilan (anuitas)
- Annual rate (tingkat bunga tahunan)
- Periods (jumlah periode pembungaan)
- Compounding (periode pembungaan, monthly untuk bulanan, annually untuk tahunan etc)
- Mode dipastikan beginning (untuk anuitas dimuka)
- Payment untuk pembayaran cicilan (anuitas)
4. Lalu pilih Present Value (PV)
Contoh 1
Hitunglah nilai sekarang dari Rp 5.000.000,00 yang diterima setiap bulan selama 5x mulai hari ini jika tingkat bunga relevan adalah 15% p.a. atau 1,25% per bulan. Hitung dengan manual, kalkulator dan microsoft excel!
Diket:
A = 5.000.000
n= 5 x
i = 15% p.a./ 1,25% bulan
Ditanya : PVDUE ?
Dijawab:
a. Manual
PVDUE ={ {\frac{1-(1+i)^{-n+1}}{i}+1} } x A
PVDUE ={ {\frac{1-(1+0,0125)^{-5+1}}{0,0125}+1} } x 5.000.000
PVDUE ={ {\frac{1-(1,0125)^{-4}}{0,0125}+1} } x 5.000.000
PVDUE ={ {\frac{1-0,951524}{0,0125}+1} } x 5.000.000
PVDUE ={ {\frac{0,048476}{0,0125}+1} } x 5.000.000
PVDUE ={ {3,878058+1} } x 5.000.000
PVDUE =4,878058 x 5.000.000
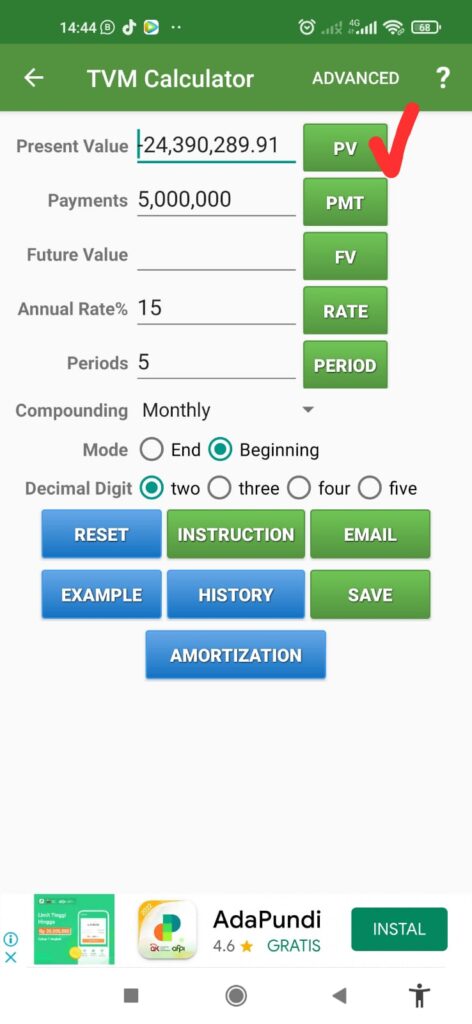
PVDUE =24.390.289,91
b. Excel
Diketahui:
Nper (jumlah periode) : 5 kali
i/Rate (tingkat bunga) : 15%p.a./ 1,25% bulan
A / Pmt (jumlah pembayaran berkala yang tetap/anuitas) : 5.000.000
=PVDUE(rate;Nper;Pmt;FV;Type)
=PVDUE(1,25%;5;5.000.000;0;1)
=-24.390.289,91
Note: Microsoft excel/kalkulator financial, ketentuan tanda positif untuk arus kas (cash flow) masuk dan tanda negatif untuk arus kas keluar tetap berlaku.
c. Financial kalkulator
Diketahui:
Nper (jumlah periode) : 5 kali
i/Rate (tingkat bunga) : 15%p.a./ 1,25% bulan
A / Pmt (jumlah pembayaran berkala yang tetap/anuitas) : 5.000.000
-
-
- Buka aplikasi financial kalkulator
- Pilih TVM
- Masukkan angka-angka diatas
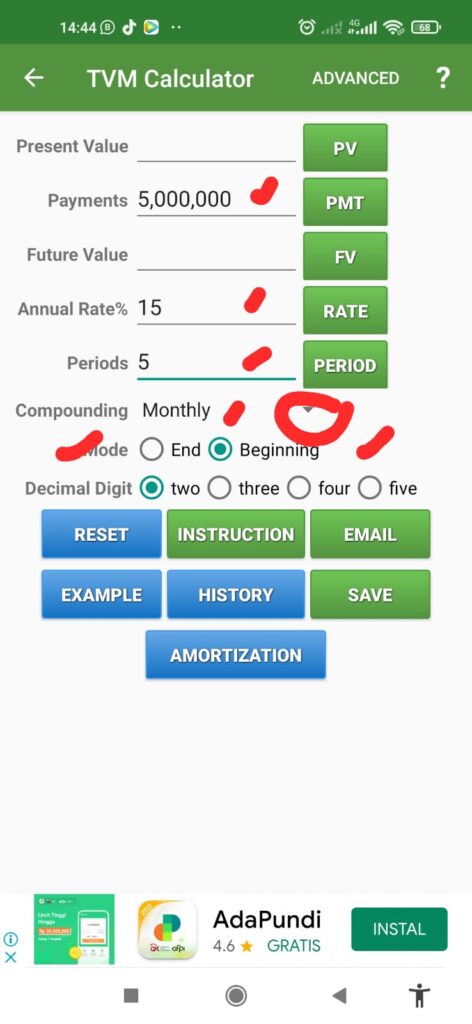
Payments/PMT/Anuitas : 5.000.0000
Annual Rate: 15
Periods : 5
Compounding: pilih yang bulanan (monthly)
Mode : pilih beginning - Tampilan sebagai berikut:
- Selanjutnya klik PV seperti gambar yang dicentang merah
- Buka aplikasi financial kalkulator
-
Menghitung Nilai Cicilan Anuitas Di Muka (A) Mengunakan Cara Manual
A=\frac{PV}{\frac{1-(1+i)^{-n+1}}{i}+1}
Menghitung Nilai Cicilan A Mengunakan Ms. Excel
=PMT(rate;Nper;Pmt;FV;Type)
Rate : tingkat bunga (misalkan dihitung per bulan maka dibagi 12 dan dikasih tanda %)
Nper : jumlah periode
PMT : jumlah pembayaran berkala yang tetap/anuitas (diberi tanda minus)
FV opsional : Nilai masa yang akan datang atau keseimbangan kas yang ingin Anda capai setelah pembayaran terakhir dilakukan. Jika fv dikosongkan, maka diasumsikan sebagai 0 (nol), yaitu, nilai pinjaman yang akan datang adalah 0.
Type : 1 jika pembayaran dilakukan pada awal periode
Menghitung Nilai Cicilan (A) Mengunakan Financial Calculator
Untuk mencari nilai sekarang menggunakan aplikasi financial calculators dapat menggunakan time value of money (TVM) dengan langkah-langkah berikut:
1. Buka aplikasi financial calculators
2. Pilih TVM calculator (pada pojok kiri atas)
3. Masukkan angka-angka yang diketahui
-
- Present value (nilai sekarang)
- Annual rate (tingkat bunga tahunan)
- Periods (jumlah periode pembungaan)
- Compounding (periode pembungaan, monthly untuk bulanan, annually untuk tahunan etc)
- Mode dipastikan beginning (untuk anuitas dimuka)
4. Klik PMT (payment) (nilai otomatis akan muncul)
Contoh 2
Sella meminjam uang ke Bank Arta sebesar Rp 25.000.000,00 dengan tingkat bunga 12%p.a. Apabila pinjaman harus dilunasi dalam waktu 24 kali cicilan yang dimulai hari ini, berapa besar cicilan per bulan?
Diket:
PV = 25.000.000
i = 12% p.a./ 1% bulan
n = 24 x
Ditanya : A ?
Dijawab:
a. Manual
A=\frac{PV}{\frac{1-(1+i)^{-n+1}}{i}+1}
A=\frac{25.000.000}{\frac{1-(1+0,01)^{-24+1}}{0,01}+1}
A=\frac{25.000.000}{\frac{1-(1,01)^{-23}}{0,01}+1}
A=\frac{25.000.000}{\frac{1-0,795442}{0,01}+1}
A=\frac{25.000.000}{\frac{0,204558}{0,01}+1}
A=\frac{25.000.000}{20,45582+1}
A=\frac{25.000.000}{21,45582}
A= 1.165.184,96
b. Ms Excel
Nper (jumlah periode) : 24 kali
i/Rate (tingkat bunga) : 12%p.a./ 1% bulan
PV : 25.000.000
=PMT(rate;Nper;PV;FV;Type)
=PMT(1%;24;25000000;0;1)
= -1.165.184,96
c. Financial Calculator
Untuk mencari nilai cicilan menggunakan aplikasi financial calculators dapat menggunakan time value of money (TVM) dengan langkah-langkah berikut:
1. Buka aplikasi financial calculators
2. Pilih TVM calculator (pada pojok kiri atas)
3. Masukkan angka-angka yang diketahui
-
-
- Buka aplikasi financial kalkulator
- Pilih TVM
- Masukkan angka-angka diatas
Present value (nilai sekarang) : 25.000.0000
Annual Rate: 12
Period : 24
Compounding: pilih yang bulanan (monthly)
Mode : pilih beginning - klik PMT (payment) (nilai otomatis akan muncul)
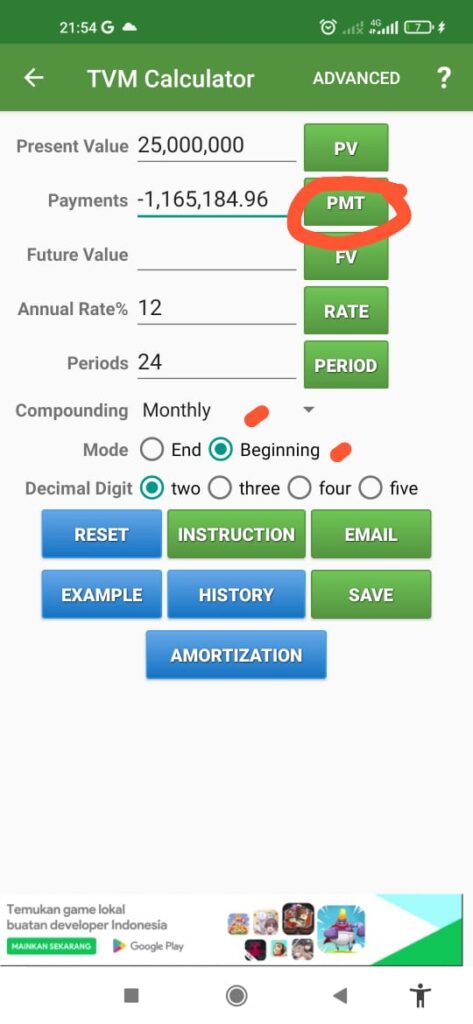
- Buka aplikasi financial kalkulator
-
Menghitung Nilai/Jumlah Periode Mengunakan Cara Manual
n=-\frac{log (1 - \frac {PV.i}{A})} {log (1+i)}
Menghitung Nilai/Jumlah Periode Mengunakan Ms. Excel
=NPER(rate;-Pmt;PV;FV;Type)
Rate: tingkat bunga (misalkan dihitung per bulan maka dibagi 12 dan dikasih tanda %)
PMT : jumlah pembayaran berkala yang tetap/anuitas (diberi tanda minus)
PV : present value
Nper : jumlah periode
FV opsional : Nilai masa yang akan datang atau keseimbangan kas yang ingin Anda capai setelah pembayaran terakhir dilakukan. Jika fv dikosongkan, maka diasumsikan sebagai 0 (nol), yaitu, nilai pinjaman yang akan datang adalah 0.
Type : 1 jika pembayaran dilakukan pada awal periode
Menghitung Nilai/Jumlah Periode Mengunakan Financial Calculator
Untuk mencari nilai sekarang menggunakan aplikasi financial calculators dapat menggunakan time value of money (TVM) dengan langkah-langkah berikut:
1. Buka aplikasi financial calculators
2. Pilih TVM calculator (pada pojok kiri atas)
3. Masukkan angka-angka yang diketahui
-
- Masukkan Present value (nilai sekarang)
- Payment untuk pembayaran cicilan (anuitas)
- Annual rate (tingkat bunga tahunan)
- Compounding (periode pembungaan, monthly untuk bulanan, annually untuk tahunan etc)
- Mode dipastikan beginning (untuk anuitas dimuka)
4. Lalu klik periods (nilai otomatis akan muncul)
Contoh 3
Tn Kamil seorang karyawan di perusahaan “Rids Organizer” yang sudah bekerja selama 20 tahun dan memperoleh uang pensiun sebesar Rp 300.000.000,00. Beliau memutuskan untuk mengambil uangnya setiap tiga bulan sekali sebesar Rp5.000.000,00 dan dimulai hari ini. Sisa uangnya di depositokan setiap 3 bulan sekali dengan bunga 5%p.a. Dalam berapa tahun depositonya akan habis?
Diket:
PV = 300.000.000 – 5.000.000 = 295.000.000
i = 5% p.a./ 1,25% /periode perhitungan (3 bulan sekali)
A = 5.000.000
Ditanya : n ?
Dijawab:
a. Manual
n=-\frac{log (1 - \frac {PV.i}{A})} {log (1+i)}
n=-\frac{log (1 - \frac {295.000.000 x 0,0125}{5.000.000})} {log (1+0,0125)}
n=-\frac{log (1 - \frac {3.687.500}{5.000.000})} {log 1,0125}
n=-\frac{log (1 - 0,7375)} {log 1,0125}
n=-\frac{log 0,2625} {log 1,0125}
n=-\frac{-0,5809} {0,0054}
n= 107,57
n= 107,57 atau jika disetahunkan maka 107 :4 = 26,8925 (26 tahun)
Setelah pengambilan yang pertama, Tn Kamil dapat mengambil sebanyak 107 kali dalam waktu 26 tahun. setelah itu Tn Kamil dapat mengambil lagi namun jumlahnya tidak melebihi dari 60%.
b. Ms. Excel
=NPER(rate;-Pmt;PV;FV;Type)
=NPER(1,25%;-5000000;300000000;0;1)
=108,6677
c. Financial Calculator
Langkah-langkah berikut:
1. Buka aplikasi financial calculators
2. Pilih TVM calculator (pada pojok kiri atas)
3. Masukkan angka-angka yang diketahui
-
-
- Buka aplikasi financial kalkulator
- Pilih TVM
- Masukkan Present value (nilai sekarang) : 300.000.0000
- Payment : 5.000.0000
- Annual Rate: 5
- Compounding: pilih yang bulanan (Quarterly)
Mode : pilih beginning (anuitas dimuka) - klik periods (nilai otomatis akan muncul) = 108,67
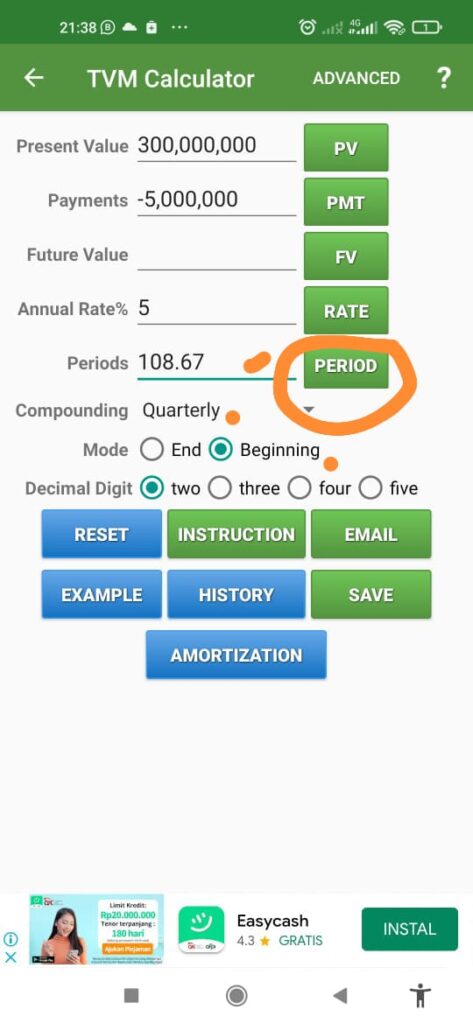
- Buka aplikasi financial kalkulator
-
Anuitas Dimuka Nilai Akan Datang (FVDUE)
Menghitung Nilai FVDUE Menggunakan Cara Manual
FVDUE = FV (ordinary annuity) x (1+i)
FVDUE = \frac{[(1+i)^n - 1]} {i} x A (1+i)
Menghitung Nilai FVDUE Menggunakan Ms. Excel
=FVDUE(rate;Nper;Pmt;FV;Type)
Rate : tingkat bunga (misalkan dihitung per bulan maka dibagi 12 dan dikasih tanda %)
Nper : jumlah periode
PMT : jumlah pembayaran berkala yang tetap/anuitas (diberi tanda minus)
FV opsional : Nilai masa yang akan datang atau keseimbangan kas yang ingin Anda capai setelah pembayaran terakhir dilakukan. Jika fv dikosongkan, maka diasumsikan sebagai 0 (nol), yaitu, nilai pinjaman yang akan datang adalah 0.
Type : 1 jika pembayaran dilakukan pada awal periode
Menghitung Nilai FVDUE Menggunakan Financial Calculator
Untuk mencari nilai sekarang menggunakan aplikasi financial calculators dapat menggunakan time value of money (TVM) dengan langkah-langkah berikut:
1. Buka aplikasi financial calculators, isi data berikut:
-
- Payment untuk pembayaran cicilan (anuitas)
- Annual rate (tingkat bunga tahunan)
- Periods (jumlah periode pembungaan)
- Compounding (periode pembungaan, monthly untuk bulanan, annually untuk tahunan etc)
- Mode dipastikan beginning (untuk anuitas dimuka)
- Payment untuk pembayaran cicilan (anuitas)
2. Lalu klik Future Value (FV)
Contoh 4
Berapa nilai yang akan datang pada akhir tahun ke 10 dari tabungan Nona Rara yang disetor sebesar Rp 1.000.000,00 setiap tahun selama 10 kali dan disetor mulai hari ini jika tingkat bunga sebesar 5%.
Diket:
n = 10
A = 1.000.000
r = 5% p.a. = 0,05
Ditanya: FVDUE?
Dijawab:
Cara Manual
FVDUE = \frac{[(1+i)^n - 1]} {i} x A (1+i)
FVDUE = \frac{[(1+0,05)^10 - 1]} {0,05} x 1.000.000 (1+0,05)
FVDUE = \frac{[(1,05)^10-1]}{0,05} x 1.050.000
FVDUE = \frac{[(1,628895-1]}{0,05} x 1.050.000
FVDUE = \frac{0,628895}{0,05} x 1.050.000
FVDUE = 12,5779 x 1.050.000
FVDUE = 13.206.795,00
Cara Menggunakan Ms. Excel
=FVDUE(rate;Nper;Pmt;FV;Type)
=FV(5%;10;1000000;0;1) atau jika angka dalam cell =FV(D13;D11;D12;0;1)
=-13.206.787,16
Untuk di excel misalnya menggunakan cell, maka pilih kolom cell yang sesuai dengan angka seperti angka rate di cell D13, periode di D11 dan Anuitas di D12.
Menghitung Nilai Cicilan Anuitas Di Muka (A) & jumlah periode (n)
A = \frac{FV} {\frac {[(1+i)^n - 1]}{i} (1+i)}
n = –\frac{log (\frac{FV.i}{A(1+i)} +1)} {log(1+i)}
Contoh 5
Tn Ali ingin memiliki uang sebesar 400.000.000 saat dia pensiun nanti, tepatnya 20 tahun lagi. Untuk tujuan itu ia akan menyisihkan gajinya setiap bulan untuk ditabung mulai hari ini karena hari ini adalah hari gajian selama 20 tahun kedepan. Berapa besar tabungan bulanan yang harus Tn Ali lakukan jika tingkat bunga 6%p.a.?
Diket:
FV = 400.000.000
n = 20 tahun x 12 = 240
r = 6% p.a. / 0,005 /bulan
Ditanya: Angsuran / Anuitas?
Dijawab:
Cara Manual
A = \frac{FV} {\frac {[(1+i)^n - 1]}{i} (1+i)}
A = \frac{400.000.000} {\frac {[(1+0,05)^{240} - 1]}{0,05} (1+0,005)}
A = \frac{400.000.000} {\frac {[(1,005)^{240} - 1]}{0,005} (1,005)}
A = \frac{400.000.000} {\frac {[(3,31020448 - 1]}{0,005} (1,005)}
A = \frac{400.000.000} {\frac {[(2,31020448 ]}{0,005} (1,005)}
A = \frac{400.000.000} {462,040896 x 1,005)}
A = \frac{400.000.000} {464,3511)}
A = 861.417,147
Cara Menggunakan Ms. Excel
=PMT(rate;Nper;PV;FV;Type)
=PMT(0,005;240;0;400.000.000;1) atau jika angka dalam cell =PMT(D1;D2;0;D3;1)
=-861.417,1482
Untuk di excel misalnya menggunakan cell, maka pilih kolom cell yang sesuai dengan angka seperti angka rate di cell D1, periode di D2 dan FV di D3.
Contoh 6
Tn Fauzan berencana untuk menabung tiap bulan sebesar Rp 500.000,00 dimulai hari ini untuk bisa mendapatkan uang sebesar Rp 25.000.000, untuk membeli sepeda motor jika tingkat bunganya adalah 6%p.a. Berapa waktu yang diperlukan Tn Fauzan untuk bisa membeli sepeda motor?
Diket:
A/PMT= 500.000
FV = 25.000.000
r = 6% p.a. / 0,005 /bulan
Ditanya: lama periode tabungan?
Dijawab:
Cara Manual
n = –\frac{log (\frac{FV.i}{A(1+i)} +1)} {log(1+i)}
n = –\frac{log (\frac{25.000.000x0,005}{500.000(1+0,005)} +1)} {log(1+0,005)}
n = –\frac{log (\frac{125.000}{500.000(1,005)} +1)} {log(1,005)}
n = –\frac{log (\frac{125.000}{502.500} +1)} {log(1,005)}
n = –\frac{log (0,248756 +1)} {log(1,005)}
n = –\frac{log (1,248756)} {log(1,005)}
n = –\frac{0,096478} {0,002166}
n = -44,542013
Cara Menggunakan Ms. Excel
=Nper(rate;PMT;PV;FV;Type)
=Nper(0,50%;-500.000;0;25.000.000;1)
=44,54
Anuitas Di Tunda (Deferred annuity)
Anuitas di tunda adalah suatu pembayaran yang dilakukan bukan akhir periode (anuitas biasa) atau dimuka, namun pembayarannya dilakukan setelah beberapa periode atau setelah m periode. Persamaan untuk anuitas di tunda:
PVm-1= \frac{[1-(1+i)^{-n}]} {i} A atau
PV= PV0 = \frac{(PV)_{m-1}} {(1+i)^{m-1}}
= \frac{\frac{[1-(1+i)^{-n}]} {i}A} {(1+i)^{m-1}}
Contoh 7
Hitung nilai sekarang dari arus kas sebesar 1.000.000 setiap tahun selama 4 x dimulai lima tahun lagi jika i = 10%p.a.
Diket:
A = 1.000.000
n = 4
r = 10% p.a. = 0,1
m= 5
Ditanya: lama periode tabungan?
Dijawab:
Cara Manual
PV = \frac{\frac{[1-(1+i)^{-n}]} {i}A} {(1+i)^{m-1}}
PV = \frac{\frac{[1-(1+0,1)^{-4}]} {0,1}1.000.000} {(1+0,1)^{5-1}}
PV = \frac{\frac{[1-(1,1)^{-4}]} {0,1}1.000.000} {(1,1)^{4}}
PV = \frac{\frac{[1-0,683]} {0,1}1.000.000} {1,4641}
PV = \frac{\frac{[0,317]} {0,1}1.000.000} {1,4641}
PV = \frac{\{3,17 x 1.000.000} {1,4641}
PV = \frac{\{3.170.000} {1,4641}
PV = 2.165.152,65351
DAFTAR PUSTAKA
Frensidy, Budi. 2019. Matematika Keuangan, Edisi keempat, Jakarta: Salemba Empat.
Leave a Reply