Pengertian Bunga Majemuk
Bunga majemuk adalah bunga yang jatuh tempo ditambahkan ke Nilai Pokok pada akhir setiap periode Compound atau periode perhitungan bunga untuk mendapatkan pokok yang baru dimana nilai pokok ditambahkan dengan nilai bunga pada periode sebelumnya.
Ilustrasinya perhitungan bunga majemuk
Tn A menyimpan uang di bank kemudian setiap akhir periode, bunga yang diperoleh tersebut tidak diambil, maka bunga itu akan bersama-sama modal menjadi modal baru yang akan berbunga pada periode berikutnya. Bunga yang diperoleh nilainya menjadi lebih besar dari bunga pada periode sebelumnya. Proses bunga berbunga pada ilustrasi ini dinamakan Bunga Majemuk.
Konsep bunga majemuk digunakan untuk perhitungan anuitas, amortisasi utang, sinking fund, perencanaan keuangan dan obligasi.
Perhitungan Bunga Majemuk
Perhitungan bunga majemuk dapat menggunakan persamaan berikut:
CI = P [(1 + r)t -1]
Dimana:
CI = Bunga majemuk atau Compound Interest
P = Pokok awal (principal)
r = tingkat bunga
t = time (waktu dalam tahun)
Fungsi tingkat bunga dalam majemuk merupakan fungsi eksponensial, karena bunga yang dihasilkan dibungakan kembali (menjadi pokok investasi) pada periode selanjutnya.
Contoh 1
Nona Nay menabung di Bank CAI sebesar Rp. 1.000.000,00 selama 3 tahun dengan bunga 12% per tahun. Hitung bunga yang diperoleh oleh Nona Nay!
Diketahui:
P = 1.000.000
t = 3 tahun
r = 12% atau 12/100=0,12
Ditanya: bunga yang diperoleh Nona Nay
Dijawab:
CI = P [(1 + r)t -1]
CI = 1.000.000 [(1 + 0,12)3 -1]
CI = 1.000.000 x 0,404928
CI = 404.928
Akumulasi tabungan Nona Nay dapat dilihat pada tabel berikut:
| Periode | Tabungan | Suku Bunga | Bunga | Total Tabungan |
|---|---|---|---|---|
| 1 | 1.000.000 | 12% | 120.000 | 1.120.000 |
| 2 | 1.120.000 | 12% | 134.400 | 1.254.400 |
| 3 | 1.254.400 | 12% | 150.528 | 1.404.928 |
| TOTAL | 404.928 | 1.404.928 |
Jadi bunga yang diperoleh oleh Nona Nay selama 3 Tahun adalah: Rp. 404.928
Contoh 2
Tn Amir meminjam uang sebesar Rp. 4.000.000,00 selama 3 tahun dengan bunga 8% per tahun. Hitung bunga yang diperoleh oleh Tn Amir!
Diketahui:
P = 4.000.000
t = 3 tahun
r = 8% atau 8/100=0,08
Ditanya: bunga yang diperoleh Tn Amir
Dijawab:
CI = P [(1 + r)t -1]
CI = 4.000.000 [(1 + 0,08)3 -1]
CI = 4.000.000 x [1,259712-1]
CI = 4.000.000 x 0,259712
CI = 1.038.848
Menghitung Nilai Akhir & Pokok Bunga Majemuk
Nilai akhir bunga majemuk kita dapat menggunakan persamaan berikut:
S = P (1 + i )n
P = S / (1 + i )n
P = S (1 + i )-n
Dimana:
S = nilai akhir
Perhitungan S dari P disebut compounding/akumulasi/ mencari nilai yang akan datang (future value)
P = nilai pokok awal (principal)
Perhitungan P dari S disebut mencari nilai sekarang atau present value
(1 + i )n = Faktor majemuk (compound factor)
n = jumlah periode perhitungan bunga (t x m)
m = frekuensi perhitungan bunga dalam setahun, yaitu 2 untuk semesteran, 4 untuk triwulan dst.
jm = tingkat bunga nominal tahunan dengan periode perhitungan m kali per tahun
i = tingkat bunga per periode perhitungan bunga (i = Jm/m)
Contoh 3
Nona Nay menabung di Bank CAI sebesar Rp. 1.000.000,00 selama 3 tahun dengan bunga 12% per tahun. Hitung nilai akhir (pokok ditambah bunga) dari tabungan Nona Nay!
Diket :
P = 1.000.000
n = t = 3 tahun (periode perhitungan bunga menggunakan tahunan)
i = 12%
Ditanya : S ?
Dijawab :
S = P (1 + i)n
S = 1.000.000 (1 + 0,12)3
S = 1.000.000 x 1,404928
S = 1.404.928,00
Contoh 4
Berapa nilai S dari P sebesar Rp. 10.000.000 jika J12=12% selama:
a. 5 tahun
b. 25 tahun
Dijawab:
a. Nilai S jika 5 tahun
Diketahui:
P = 10.000.000
J12 = 12%
i = 12%/12 = 1% = 0,01
n = 5 x 12 = 60 bulan
Diketahui:
S = P (1 + i)n
S = 10.000.000 (1 + 0,01)60
S = 10.000.000 x 1,817
S = 18.166.966,99
b. Nilai S jika 25 tahun
Diketahui: n = 25 x 12 = 300 bulan
S= P (1 + i)n
S = 10.000.000 (1 + 0,01)300
S = 197.884.662,62
Jika dihitung menggunakan bunga sederhana maka:
SI = P r t
SI = 10.000.000 x 12% x 25 = 30.000.000
Total bunga majemuk dari Rp. 10.000.000 dengan J12=12% selama 25 tahun adalah 187.884.662,62 atau lebih dari 18 kali nilai pokok awal. Jika metode bunga sederhana digunakan, jumlah bunga hanya Rp. 30.000.000 jauh dibawah hasil dengan bunga majemuk.
Contoh 5
Seorang karyawan menyimpan uangnya sebesar Rp. 4.000.000 dalam sebuah bank yang memberikan bunga sebesar 12% diperhitungkan dan dikreditkan harian. Berapa bunga yang dihasilkan selama tahun pertama?
Diketahui:
n = 365
Ditanya: CI ?
Dijawab :
CI = P (1 + i)n – P
CI = 4.000.000 (1 + 0,00033)365 –4.000.000
CI = (4.000.000 x 1,127475) – 4.000.000
CI = 509.898,46
Cara II:
S = P (1 + i)n
S = 4.000.000 (1 + 0,00033)365 x 1
S = 4.000.000 (1,00033)365
S = 4.000.000 x 1,1274746
S = 4.509.898,46
Untuk mencari bunga maka nilai akhir dikurangi dengan pokok
CI = S-P
CI = 4.509.898,46 – 4.000.000
CI = 509.898,46
Total bunga majemuk pada tahun pertama adalah 509.898,46
Bunga Efektif dan Bunga Nominal
Tingkat bunga nominal adalah tingkat bunga yang selalu dinyatakan per tahun atau per annum (p.a.). Dalam transaksi kredit, mayoritas suku bunga dinyatakan dalam tahunan, namun pelaksanaanya dihitung dengan periode pemajemukan lebih dari satu kali dalam setahun.
Contoh saja suku bunga 10% per tahun, namun periode perhitungan pemajemukan bunga dihitung setiap 6 bulan yaitu 5%. Suku bunga 10% disebut suku bunga nominal (nominal rate), sedangkan pemajemukan setiap 6 bulan yaitu 5% disebut tingkat bunga efektif.
Suku bunga nominal (r) merupakan perkalian tingkat suku bunga (i) per periode dengan jumlah pemajemukan sebanyak m kali dalam setahun. Suku bunga nominal dinyatakan:
r = i x m atau i = r/m
Suku bunga efektif adalah suku bunga sesungguhnya dalam satu tahun yang tepat dibayarkan terhadap sejumlah uang yang kita simpan atau pinjamkan. Suku bunga efektif dapat dinyatakan dengan persamaan berikut:
J1 = (1 + i)m-1
Contoh 6
Hitung tingkat bunga efektif j1 yang ekuivalen dengan:
a. j2 = 10%
b. j12 = 12%
Lakukan perhitungan dengan cara manual:
J1 = 0,1025
b. j12 = 12%
J1 = 0,1268
J1 = 12,68%
Hitung tingkat bunga efektif j1 yang ekuivalen dengan:
a. j365 = 12%
b. j12 = 12%
c. j6 = 12%
d. j2 = 12%
Lakukan perhitungan dengan cara manual:
a. j365 = 12%
J1 = 0,1275
J1 = 12,75%
b. j12 = 12%
J1= (1 + 0,12/12)12-1
J1 = 0,1268
J1 = 12,68%
c. j6 = 12%
J1= (1 + 0,12/6)6-1
J1 = 12,62%
J1 = 0,1236
J1 = 12,36%
Semakin besar nilai m atau compounding period per year pada bunga nominal, semakin besar bunga efektif yang dihasilkan. Hal ini karena pada bunga majemuk, bunga yang jatuh tempo ditambahkan ke nilai pokok pada akhir setiap periode compound atau periode perhitungan bunga untuk mendapatkan pokok yang baru. Dengan m atau compounding period per year yang besar, frekuensi perhitungan bunga semakin besar sehingga bunga efektif menjadi semakin besar pula.
Menghitung Nilai Sekarang
Proses mencari nilai sekarang (present value) (P) atau nilai pokok awal, atau nilai yang didiskontokan (discounted value) disebut pendiskontoan (discounting). Persamaan untuk mencari P adalah sebagai berikut:
Contoh 8
Dengan menggunakan J12 = 12%, hitung nilai diskonto atau nilai yang didiskontokan dari uang sejumlah 100.000.000 yang jatuh tempo 10 tahun lagi.
Diketahui:
S = 100.000.000
n = 10 tahun x 12 = 120
i = 12%/12 = 1% = 0,01
Dijawab:
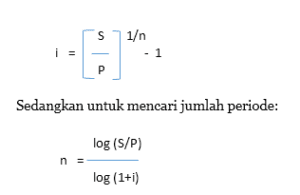
Menghitung Tingkat Bunga dan Jumlah Periode
Untuk mencari tingkat bunga, kita dapat menggunakan persamaan berikut:
Contoh 9
Berapa tingkat bunga j12 yang dapat membuat sejumlah uang menjadi tiga kali lipat dalam 12 tahun?
Jawab:
n = 12 x 12
Kita asumsikan uang tersebut x maka:
x (1+i)144 = 3x
(1+i)144 = 3
(1+i) = 3 1/144
i = 3 1/144 – 1
i = 0,00765843
j12 = 12 x i
j12 = 12 x 0,00765843
j12 = 0,0919 atau 9, 19%
Contoh 10
Berapa lama waktu yang diperlukan untuk membuat uang sebesar Rp. 5.000.000 menjadi 8.500.000 dengan J12= 12%?
Diketahui:
P = 5.000.000
S = 8.500.000
i = 12%/12 = 1% = 0,01
Dijawab:
Jadi lama waktu yang diperlukan untuk membuat uang sebesar Rp. 5.000.000 menjadi 8.500.000 adalah 53, 3277 bulan atau 4 tahun 5 bulan 10 hari
Aturan 72 untuk menggadakan Uang
Untuk mengetahui berapa lama waktu yang diperlukan untuk menggandakan uang atau membuat uang jadi dobel atau dua kalinya jika diinvestasikan dalam produk keuangan yang memberikan return tertentu, kita dapat menghitung jumlah periode dengan persamaan berikut:
Atau kita dapat menggunakan aturan praktis (rule of thumb) yang memberikan hasil yang tak jauh berbeda, yaitu aturan 72.
Jika seseorang ingin investasinya berlipat dua dalam 6 tahun, maka return tahunan yang diperolehnya adalah 12% p.a.
Pemajemukan Kontinyu (Continuous Compounding)
Semakin besar frekuensi perhitungan bunga semakin besar, semakin besar bunga efektif yang dihasilkan misalnya dari frekuensi tahunan, semesteran, bulanan, mingguan, harian, perjam, per menit, per detik sampai tak terhingga. Pemajemukan kontinyu adalah banyaknya periode pembungaan dalam setahun adalah tak terhingga. Persamaan Bunga majemuk biasa (compound interest) :
FV = PV ert
Untuk mencari r atau t sebagai berikut:
FV = PV(1+i)n = PV(1+i)t = PV ert
ln(1+i)t = ln ert
ln(1+i) = ln er
ln(1+i) = r ln e
ln(1+i) = r x (1)
r = ln (1+i)
(1+i)t = ert
(1+i) = ert
i = er – 1
Dimana:
FV = future value
PV = present value
e = bilangan eksponensial yang besarnya 2,718281828
r = tingkat bunga kontinu
i = tingkat bunga diskrit
t = periode waktu
Contoh
Berapa tingkat bunga kontinu (r) yang ekuivalen dengan tingkat bunga diskrit (i) 10% p.a.?
r = In (1+i)
r = In (1+10%)
r = 0,0953 atau 9,53%
Contoh
Hitunglah i yang ekuivalen dengan r=12% p.a?
i = er– 1
i = e12% – 1
i = 2,71828182812%-1
i = 12,75%
Contoh
Sebuah deposito sebesar Rp 10.000.000 dapat memberikan pendapatan bunga sebesar Rp 5.600.000 selama 36 bulan. Hitung tingkat bunga nominal tahunnannya apabila:
a. Perhitungan bunga tahunan
b. Continuous compounding
Diketahui:
S = 15.600.000
P = 10.000.000
t= 36 bulan = 36/12 = 3 tahun
Jawab
a. Perhitungan bunga tahunan
S = P (1+i) n
(1+i) n = S/P
(1+i) 3 = 15.600.000 / 10.000.000
(1+i) 3 = 1,56
i = ∛(1,56−1)
= 0,159778
= 15,98 %
b. Continuous compounding
S = P e rt
e rt = S/P
e rt = 15.600.000 / 10.000.000
e rt = 1,56
ln e rt = ln 1,56
rt len e = 0,444685821
3 r x (1) = 0,444685821
3r = 0,444685821
r = 0,148228607
r = 14,82 %
SOAL dan PEMBAHASAN
Untuk lebih memahami bunga majemuk, anda perlu mempelajari soal dan pembahasan di berikut ini: klik disini
LATIHAN SOAL
Untuk lebih mendalami bunga majemuk kerjakan contoh soal berikut ini: klik disini
DAFTAR PUSTAKA



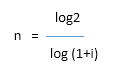
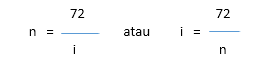
Leave a Reply